今日題目

題目連結：53. Maximum Subarray
題目主題：Array, Divide and Conquer, Dynamic Programming

簡單說說 Divide and Conquer

Divide and Conquer的主要概念就是Divide 分割、Conquer 克服這兩個，意思是會把一個大問題一層一層的分割成小範圍的問題，一直到不能再分割為止，之後再一層一層的往上克服拿到整個大問題的答案。

下面是一個常見的例子，有一種排序方法叫Merge Sort，是用Divide and Conquer概念來實作的，

Divide: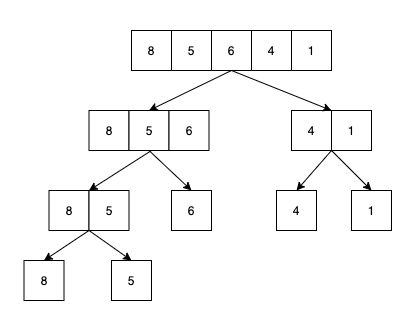

一層一層向下去切割成小範圍，直到不能再切割。

Conquer: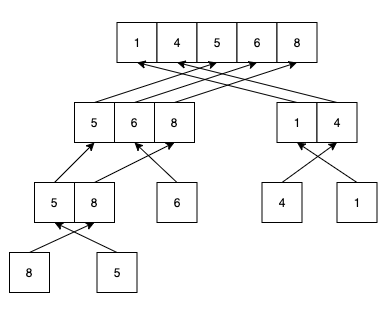

一層一層往上去解決目前的問題，這邊解決的問題就是排序，每往上一層就會排序好一個範圍，走到最上層就會將整個陣列裡面的數字從小到大排序好。

題目解說

建議可以看看LeetCode原本的題目說明，這邊是用我的方式說明題目，參考就好。

題目會給一個 nums 數字陣列，目的是要找出 nums 中每個連續的子集合總和後最大的值，最終回傳這個最大的總和值。

約束：

• 1 <= nums.length <= 10的5次方
• -10的4次方 <= nums[i] <= 10的4次方

範例1

輸入: nums = [-2,1,-3,4,-1,2,1,-5,4]
輸出: 6
解說: 
列出全部的連續子集合可能會有點多，這邊只舉幾個例子:
[-2] = -2
[-2,1,-3,4] = 0
[4,-1,2,1] = 6
[2,1,-5,4] = 2
[-2,1,-3,4,-1,2,1,-5,4] = 1
上面都是連續的子集合的例子，每個加總後可以看到[4,-1,2,1]總和的6最大，因此最後輸出 6。

範例2

輸入: nums = [1]
輸出: 1
解說: 因為只有一個 1，因此最大也一定是 1。

範例3

輸入: nums = [5,4,-1,7,8]
輸出: 23
解說: 這個例子最大的就是[5,4,-1,7,8]加總後的23，因此最後輸出23。

建議到這邊先停下來，嘗試自己解解看，若沒有想法可再繼續走下去。

解題的想像

文字描述

1. 寫一個遞迴方法，傳入nums、開始位置、結束位置，每一次呼叫會處理以下：
   • 用開始位置及結束位置找中間位置。
   • 將目前範圍 nums 以中間位置開始切成左邊及右邊兩個子集合。
   • 取得左邊連續子集總和後的最大值。
   • 取得右邊連續子集總和後的最大值。
   • 取的中間連續子集總和後的最大值。
   • 最後向上回傳左邊、右邊、中間之中最大的總和值。
2. 這個遞迴方法，會一直切到不能再切割為止，最終全部走完會回傳所有連續子集總和後的最大值。

圖解過程

範例：nums = [-3, 4, -1, 2, 1, -5, 4, -2]

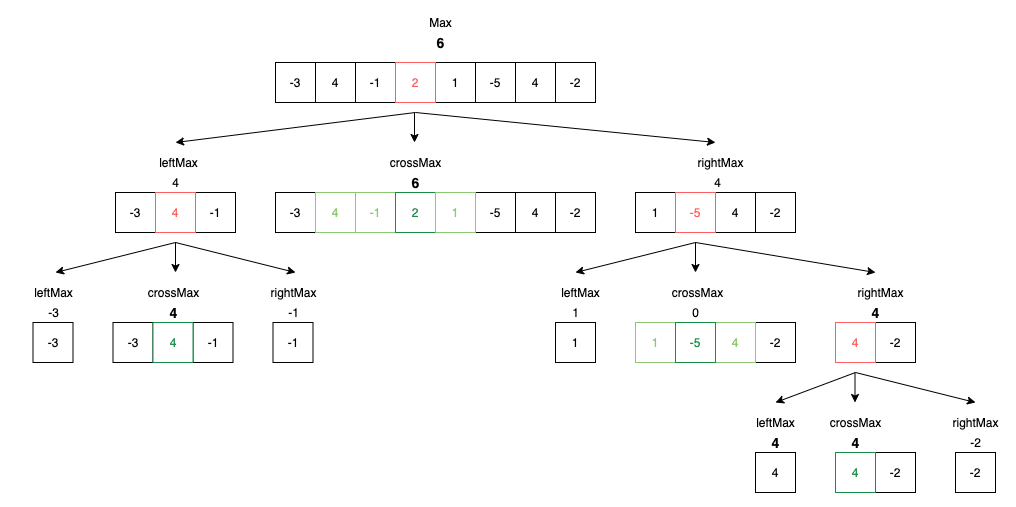
上圖中是使用Divide and Conquer的運作過程，紅色的方框是每一次的切割點每往下一層會切成三個部份，leftMax、crossMax、rightMax，可以先特別看看crossMax的部份綠色方框代表現在crossMax這個範圍總和最大的子集。

接著，每一層都會得到一個粗體的數字代表是目前這一層範圍的子集合中最大的總和，將這個值在往上傳，跑回到最上層就可以拿到整體範圍的Max值，就是這個範例的答案了。

若因為沒想法而走到這邊，建議看完想像以後再給自己一次機會試一次。

程式碼撰寫

class Solution:
    # 取得中間子集合最大值
    def getCrossMax(self, nums, startIndex, middleIndex, endIndex):
        crossLeft = 0
        crossRight = 0
        tmpValue = 0
        # 從中間向左走最大子集合
        for i in range(middleIndex-1, startIndex-1, -1):
            tmpValue += nums[i]
            crossLeft = max(tmpValue, crossLeft)        
        tmpValue = 0
        # 從中間向右走最大子集合
        for i in range(middleIndex+1, endIndex+1):
            tmpValue += nums[i]
            crossRight = max(tmpValue, crossRight)
        # 將左中右的值都相加後，為中間子集合最大值
        return crossLeft + nums[middleIndex] + crossRight
    
    # 取得最大值
    def getMax(self, nums, startIndex, endIndex):
        # 若開始位置超過結束位置，代表剩一個值，回傳當下的值
        if startIndex >= endIndex:
            return nums[startIndex]
        # 找到中間位置
        middleIndex = int((startIndex + endIndex)/2)
        
        # 取得左邊子集合最大值
        leftMax = self.getMax(nums, startIndex, middleIndex-1)
        # 取得右邊子集合最大值
        rightMax = self.getMax(nums, middleIndex+1, endIndex)
        # 取得中間子集合最大值
        crossMax = self.getCrossMax(nums, startIndex, middleIndex, endIndex)
        # 找到目前範圍的最大值
        return max(leftMax, rightMax, crossMax)
        
    def maxSubArray(self, nums: List[int]) -> int:
        return self.getMax(nums, 0, len(nums)-1)

希望您今天能瞭解到...

1. Divide and Conquer 基本概念
2. 53. Maximum Subarray 使用Divide and Conquer的解法

若內容有什麼問題或建議歡迎一起交流：）
感謝您今天願意花時間看完這篇文章~~~~

Next：53. Maximum Subarray - Dynamic Programming